Given the abundance of constraints now available for the determination of the CKM parameters, ρ and η, we have the possibility of removing from the fitting procedure the use of the hadronic parameters coming from lattice calculations, letting them as free parameters of the fit. In this way we can compare the uncertainty obtained on a given quantity through the UT fit to the present theoretical error on the same quantity. Practically to obtain the a-posteriori p.d.f. for a given hadronic quantity, we perform the UT fit imposing as input an uniform distribution in a range much larger than the expected interval of values assumed for the quantity itself. This approach allows for the possibility of making a full UT analysis without relying at all on theoretical calculations of hadronic matrix elements for which there was a long debate about the treatment of values and error distributions. We can then extract from the combined experimental measurements the value of B_K and of the B⁰ mixing amplitudes f_B(s,d)√B_B(s,d) (or equivalently f_Bs√B_Bs and ξ) and compare them to the theoretical predictions.

It is important to stress that, as firstly stated in this UTfit paper and contrary to what was previously done, the bounds on Δm_d and Δm_s enter into the analysis through ξ and f_Bs√B_Bs, which are the parameters better determined from the lattice and whose systematic uncertainties are mostly uncorrelated. This strategy changes the equations that relate the experimental quantities to ρ and η

Below we show the one-dimensional distributions and the numerical results for the various lattice quantities obtained using in the fit all the available constraints on the angles (α, β, γ that is the UTangle fit) plus the one coming from the semi-leptonic decays (V_ub/V_cb). We exclude those constraints requiring the lattice QCD calculations (Δm_d, Δm_s, and ε_K). In the table at the bottom of the page, we compare the lattice inputs used in the UTfit analysis with the predictions obtained from the angles and angles+V_ub/V_cb fits.

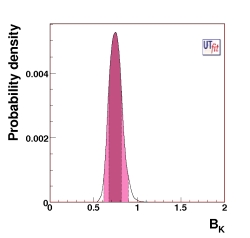
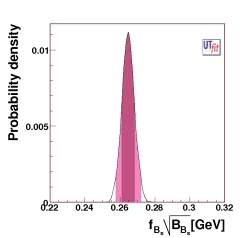
(EPS) [JPG] p.d.f. of BK from the UTangle + Vub/Vcb BK = 0.74 ± 0.07	(EPS) [JPG] p.d.f. of fBs√ BBs from the UTangle + Vub/Vcb fBs√ BBs = (264.7 ± 3.6) MeV
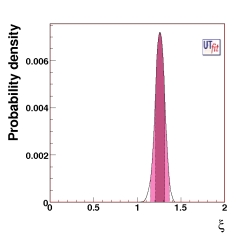
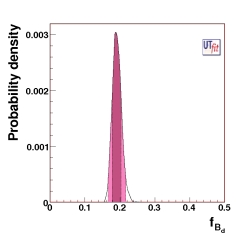
(EPS) [JPG] p.d.f. of ξ from the UTangle + Vub/Vcb ξ = 1.26 ± 0.05	(EPS) [JPG] p.d.f. of fB from the UTangle + Vub/Vcb fB = (191 ± 13) MeV
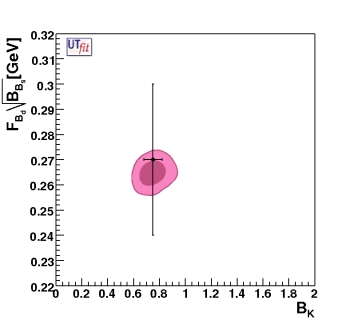
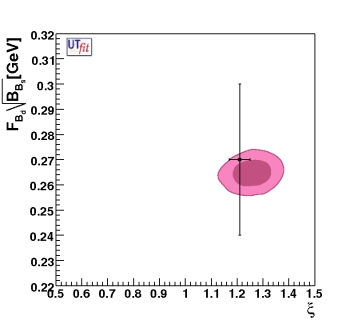
(EPS) [JPG] The 68% and 95% contours in the fBs√BBs(MeV)- BK plane	(EPS) [JPG] The 68% and 95% contours in the fBs√BBs(GeV)-ξ plane
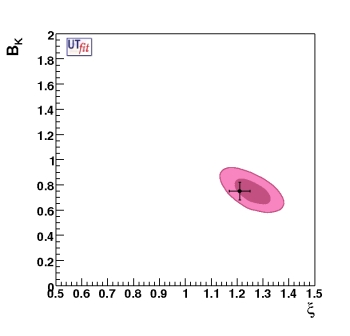
(EPS) [JPG] The 68% and 95% contours in the BK-ξ plane

We quote below the numerical results for the lattice QCD parameters in two different UT fit configurations: the one described above that is using only the angles (UTangle) and the one including also the V_ub/V_cb constraint from the semi-leptonic decays (UTangle + V_ub/V_cb). For reference also the lattice QCD experimental values are reported in the last column (ref. arXiv:0807.4605v1 [hep-lat]).