 (EPS) [JPG] |
 (EPS) [JPG] |
||||
|
|
||||
 (EPS) [JPG] |
 (EPS) [JPG] |
Thanks to the abundance of experimental information, one can determine stringent bounds to NP parameters, simultaneously to the determination of the UT parameters. Starting from the New Physics Free determination of ρ and η, we explore, in a model-independent approach, the possible contributions of NP effects to Bd-Bd, Bs-Bs and K0-K0 mixing. Each of these processes can be parameterized in terms of only two new parameters, which we choose to quantify the difference of the amplitude, in absolute value and phase, with respect to the SM one. Thus in the case of Bq-Bq mixings, we define
|
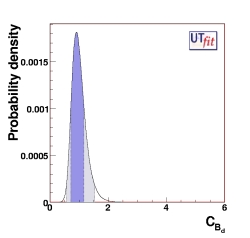
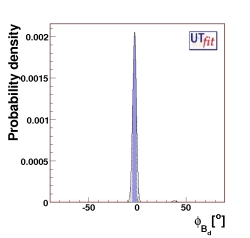
where HeffSM includes only the SM box diagram, while Hefffull includes also the NP contributions. In the second equation we also introduce φqSM where φdSM = β and φsSM = -βs These definitions imply that the mass differences and the CP asymmetry are related to the SM counterparts by
| Δmd=CBd ⋅ ΔmdSM | Δms=CBs ⋅ ΔmsSM |
| βexp = βSM + φBd | αexp = αSM - φBd |
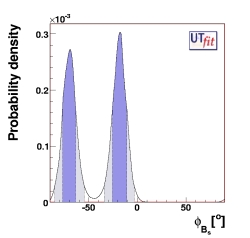
| βsexp = βsSM - φBs |
We can also write
|
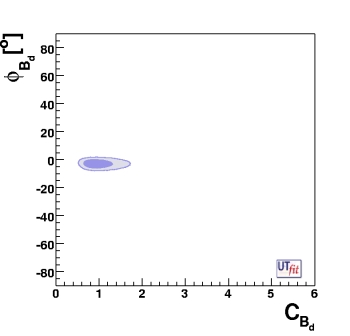
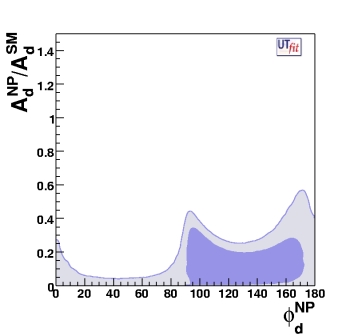
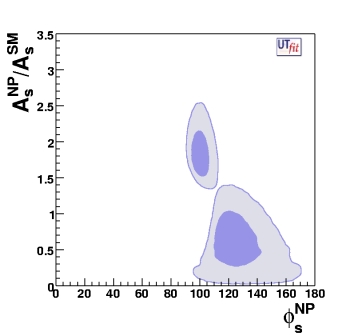
and given the p.d.f. for CBd and φBd, we can derive the p.d.f. in the (ANP/ASM) vs φNP plane.
 (EPS) [JPG] |
 (EPS) [JPG] |
||||
|
|
||||
 (EPS) [JPG] |
 (EPS) [JPG] |
 (EPS) [JPG] |
 (EPS) [JPG] |
||||
|
|
||||
 (EPS) [JPG] |
 (EPS) [JPG] |
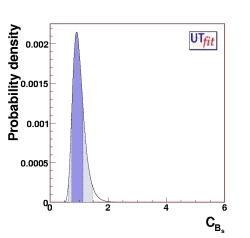
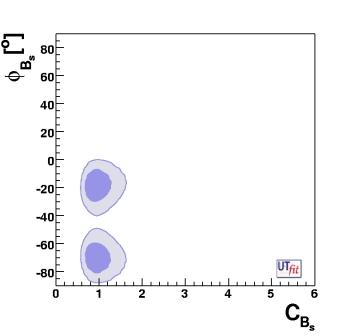
The values of CBd and CBs show an an interesting correlation (see figure below). This correlation that is present in the general analysis, is due to the fact that lattice QCD determines quite precisely the ratio ξ2 of the matrix elements entering Bd and Bs mixing amplitudes.
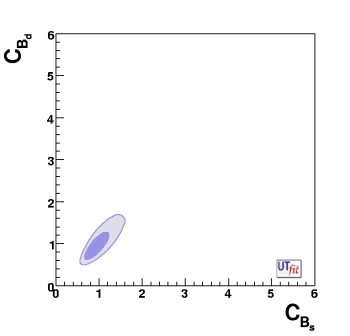 (EPS) [JPG] |
The AM+NP amplitude for K0-K0 mixing can be written in a similar way:
|
|
This definition implies a simple relation for |εK|:
| |εK|=CεK|εK|SM |
With respect to the SM analysis, some constraint is modified and new constraints are added.
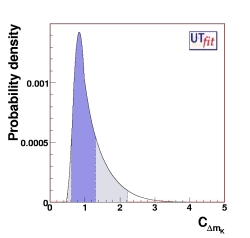 (EPS) [JPG] |
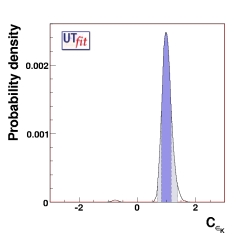 (EPS) [JPG] |
||||
|
|
||||
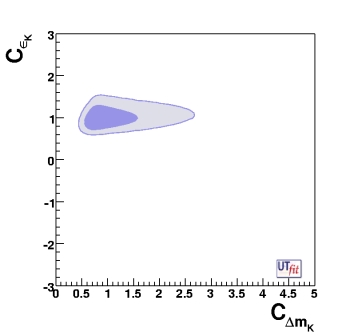 (EPS) [JPG] |
|||||
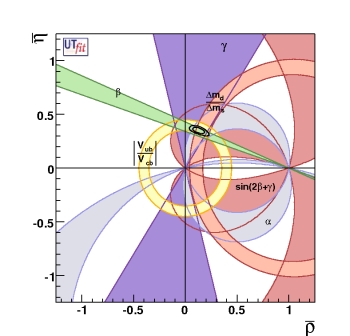
The NP analysis shown above also provides the values of the CKM parameters, from which the angles and sides of the UT can be computed. We list below the result obtained from the simultaneous fit. These values represent the allowed ranges in this generalized framework. We found only one favoured solution, corresponding to the result of the Standard Model fit, while the second region, corresponding to the UT with its vertex in the third quadrant and implying sizable New Physics effects in the Bd sector, present in the previous version of this analysis is now excluded at 95% probability.
|
Results of NP generalized analysis
|
|
Parameter
|
68% probability Region
|
|
ρ
|
0.177 ± 0.044 |
|
η
|
0.360 ± 0.031 |
|
α
|
(92 ± 7)o |
|
β
|
(24.7 ± 1.8)o |
|
γ
|
(63 ± 7)o |
|
sin2β
|
0.734 ± 0.038 |
|
sin2βs
|
0.038 ± 0.003 |
|
105 Re λt
|
-31.7 ± 1.8 |
|
105 Im λt
|
14.1 ± 1.2 |
|
103|Vub|
|
3.87 ± 0.23 |
|
102|Vcb|
|
4.12 ± 0.05 |
|
103|Vtd|
|
8.3 ± 0.5 |
|
Vtd/Vts|
|
0.206 ± 0.012 |
|
Rb
|
0.404 ± 0.025 |
|
Rt
|
0.897 ± 0.047 |
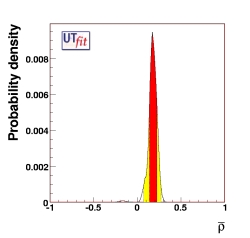 (EPS) [JPG] |
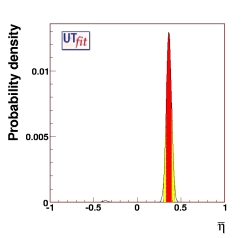 (EPS) [JPG] |
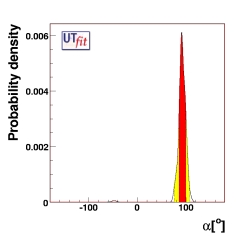 (EPS) [JPG] |
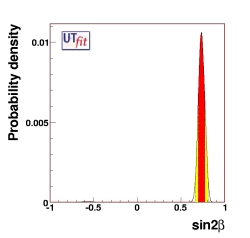 (EPS) [JPG] |
 (EPS) [JPG] |
 (EPS) [JPG] |
 (EPS) [JPG] |
||
It is possible to generalize the full UTfit beyond the Standard Model to all those NP models characterized by Minimal Flavour Violation, i.e. having quark miking ruled only by the Standard Model CKM couplings. In fact, in this case no additional weak phases are generated and several observables entering into the Standard Model fit (the tree-level processes and the measurement of angles through the use of time dependent CP asymmetries) are not affected by the presence of New Physics. The only sizable effect we are sensitive to is a shift of the Inami-Lim function of the top contribution in meson mixing. This means that in general εK and Δmd cannot be used in a common SM and MFV framework, but any New Physics contribution disappear in the case of Δmd/Δms. So, simply removing the information related to εK and Δmd from the full UTfit one can obtain a more precise determination of the Universal Unitarity Triangle, which is a common starting point for the Standard Model and any MFV model.
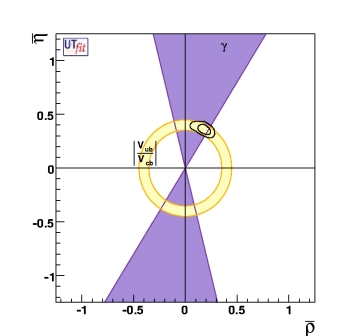
 (EPS) [JPG] Result of UUT fit on the (ρ, η) plane |
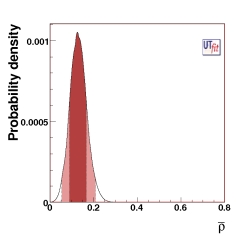 (EPS) [JPG] ρ = 0.128 ± 0.038 from UUT fit |
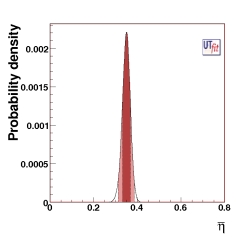 (EPS) [JPG] η = 0.350 ± 0.018 from UUT fit |
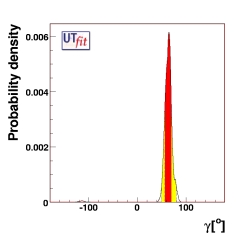
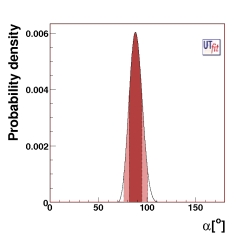 (EPS) [JPG] PREDICTIONS: α = (88 ± 6)o from UUT fit |
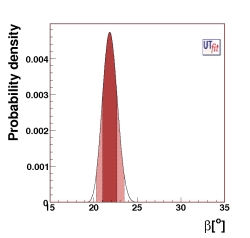 (EPS) [JPG] PREDICTIONS: β = (21.8 ± 0.8)o from UUT fit |
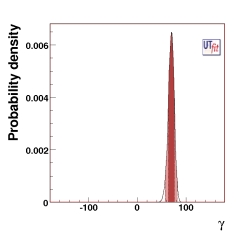 (EPS) [JPG] PREDICTIONS: γ = (70 ± 6)o from UUT fit |
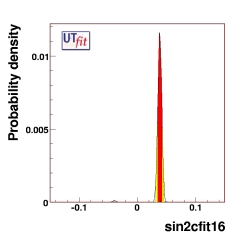
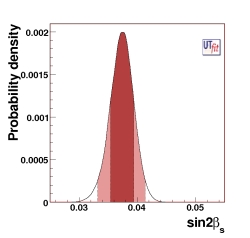 (EPS) [JPG] PREDICTIONS: sin2βs = 0.037 ± 0.002 from UUT fit |
One has to notice that the precision on ρ and η is in practise the same than in the full UTfit. This means that one can go forward in the study of MFV, using the two neglected informations (εK and Δmd) to bound the scale of New Physics. In fact, the expected contribution is a shift of S0, the Inami-Lim function associated to top contribution in box diagrams. The shift can than we translated in terms of the tested energy scale for New Particles, using a simple dimensional argument.
|
where δS0 is the shift, a is a parameter related to Wilson coefficients of the effective Hamiltonian, Λ is the New Physics scale and Λ0=Ytsin2(θW)MW/α ∼ 2.4 TeV is the reference EW scale. One can extract Λ0 in two different scenarios:
Here we show the result in terms of the output distribution of δS0 (δS0B and δS0K) in the case of models with low/moderate (large) values of tanβ and we give the output value in terms of the tested energy scales, quantified at the 95% Probability.
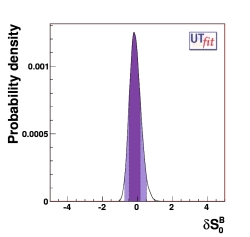 (EPS) [JPG] δS0 = -0.16 ± 0.32 |
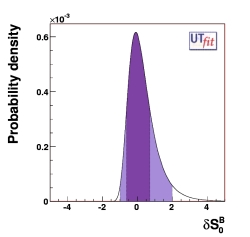 (EPS) [JPG] δS0B = 0.05 ± 0.67 |
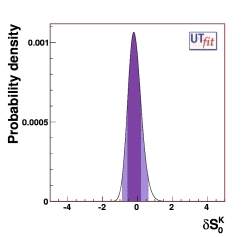 (EPS) [JPG] δS0K = -0.18 ± 0.37 |
|
for small tanβ |
for large tanβ |
|