sin(2β+γ) can be extracted from time dependent asymmetries in B decays to D^(*) π final states, looking at the interference effect between the decay amplitudes implying b→c and b→u transitions. The time dependent rates can be written as:

where S and C parameters are defined as

and r and δ are the absolute value and the phase of the amplitude ratio A(B⁰→D^-π⁺) / A(B⁰→D^-π⁺). It is clear that the ratio r is quite small being of the order of λ |V_ub/V_cb| ~0.02. Analogous expressions can be written for D^(*) π decays.

BaBar and Belle provided three different measurements of this channel, with total (both) or partial (BaBar only) reconstruction of the final state.
In hep-ex/0303030 O. Long et al. showed the existence of a correlation between tag side and reconstruction side in time dependent CP measurements at the B-Factories. This is related to the fact that interference between b→c and b→u transitions in B→D X decays can occur also in the tag side. In the case of sin(2β+γ) this is particularly important, since the effect studied on reconstruction side is exactly the same. In order to include it in the fit, S and S entering the time dependent rates are replaced by

where r' and δ' are the analogous of r and δ for the tag side. It is important to stress the fact that this interference effect on the tag side can not occur in case the B meson are tagged using semileptonic decays. In other words, r'= 0 when only semileptonic decays are considered. In the following we will consider the fitted quantities a, c(lepton),a^(*) and c^(*)(lepton), which are functions of r,r^(*), δ, δ^(*) and 2β+γ.

With the present experimental data, a determination of 2β+γ cannot be obtained from D^(*)π(ρ) modes alone. The number of free parameters exceeds the available constraints as shown by equations above. Without further input, one can only find correlations among 2β+γ and the hadronic parameters. The only information one can extract in a model independent way comes from the r vs 2β+γ correlation plot for the various channels.

(EPS), [JPG] Distribution of r(Dπ) vs 2β+γ

(EPS), [JPG] Distribution of r(D*π) vs 2β+γ

(EPS), [JPG] Distribution of r(Dρ) vs 2β+γ

An independent information on the hadronic parameters would allow a determination of 2β+γ. For instance, assuming SU(3) flavour symmetry and neglecting annihilation contributions, one can estimate BR(B⁰ → D^*-π⁺) from BR(B⁰ → D_s^*-π⁺), up to a theoretical uncertainty related to SU(3) breaking effect and to the size of annihilation contributions. We take into account the combination of these two effects assigning a ± 100% flat error to be convolved with the experimental one. In this way, we obtain as input values r(D*π) = 0.015 ± 0.006 ± 0.015 (where the first error is statistical and the second is the flat theoretical error). The same approach for the other two channels give r(Dπ) = 0.020 ± 0.003 ± 0.020 and r(Dρ) = 0.003 ± 0.006 ± 0.003. Under these assumptions, we get a constraint on 2β+γ as shown in the figure below.

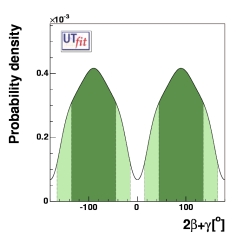
(EPS), [JPG] constraint on 2β+γ combining Dπ, D*π and Dρ 2β+γ = (± 90 ± 46)o

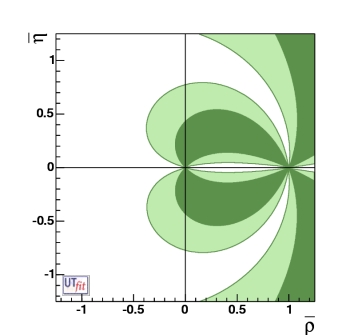
(EPS), [JPG] constraint on the (ρ ; η) plane combining Dπ D*π and Dρ.

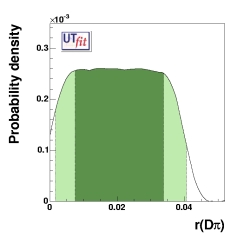
(EPS), [JPG] prior distribution for r(Dπ) r(Dπ) = 0.021 ± 0.013 ([0.002,0.041] @ 95% Prob.)

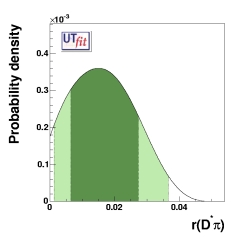
(EPS), [JPG] prior distribution for r(D*π) r(D*π) = 0.017 ± 0.010 ([0.001,0.037] @ 95% Prob.)

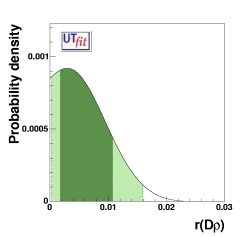
(EPS), [JPG] prior distribution for r(Dρ) r(Dρ) = 0.006 ± 0.004 ([0.000,0.016] @ 95% Prob.)

We would like to thank Riccardo Faccini, Marie Legendre, Cecilia Voena and Marco Zito from BaBar Collaboration for the useful discussions on the interpretation of experimental results.